Книга: Учебное пособие по курсу «Нейроинформатика»

Определение показателей значимости через градиент

Определение показателей значимости через градиент

Нейронная сеть двойственного функционирования может вычислять градиент функции оценки по входным сигналам и обучаемым параметрам сети.

Показателем значимости параметра при решении q-о примера будем называть величину, которая показывает насколько изменится значение функции оценки решения сетью q-о примера если текущее значение параметра wpзаменить на выделенное значение w^•p. Точно эту величину можно определить произведя замену и вычислив оценку сети. Однако учитывая большое число параметров сети вычисление показателей значимости для всех параметров будет занимать много времени. Для ускорения процедуры оценки параметров значимости вместо точных значений используют различные оценки [33 , 65 , 91]. Рассмотрим простейшую и наиболее используемую линейную оценку показателей значимости. Разложим функцию оценки в ряд Тейлора с точностью до членов первого порядка:

где H⁰_q — значение функции оценки решения q-о примера при w^•=w. Таким образом показатель значимости p-о параметра при решении q-о примера определяется по следующей формуле:

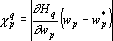
Показатель значимости (1) может вычисляться для различных объектов. Наиболее часто его вычисляют для обучаемых параметров сети. Однако показатель значимости вида (1) применим и для сигналов. Как уже отмечалось в главе «Описание нейронных сетей» сеть при обратном функционировании всегда вычисляет два вектора градиента — градиент функции оценки по обучаемым параметрам сети и по всем сигналам сети. Если показатель значимости вычисляется для выявления наименее значимого нейрона, то следует вычислять показатель значимости выходного сигнала нейрона. Аналогично, в задаче определения наименее значимого входного сигнала нужно вычислять значимость этого сигнала, а не сумму значимостей весов связей, на которые этот сигнал подается.

Оглавление книги