Книга: Учебное пособие по курсу «Нейроинформатика»

Сеть Кохонена

Сеть Кохонена

Сети Кохонена [131, 132] (частный случай метода динамических ядер [224, 262]) являются типичным представителем сетей решающих задачу классификации без учителя. Рассмотрим пространственный вариант сети Кохонена. Дан набор из m точек {xp} в n-мерном пространстве. Необходимо разбить множество точек {xp} на k классов близких в смысле квадрата евклидова расстояния. Для этого необходимо найти k точек ?^l таких, что

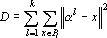
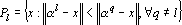
Существует множество различных алгоритмов решения этой задачи. Рассмотрим наиболее эффективный из них.

1. Зададимся некоторым набором начальных точек ?^l.

2. Разобьем множество точек {xp} на k классов по правилу

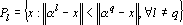
3. По полученному разбиению вычислим новые точки ?^l из условия минимальности

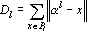
Обозначив через |P_i| число точек в i-ом классе, решение задачи, поставленной на третьем шаге алгоритма, можно записать в виде

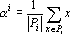
Второй и третий шаги алгоритма будем повторять до тех пор, пока набор точек ?^l не перестанет изменяться. После окончания обучения получаем нейронную сеть, способную для произвольной точки x вычислить квадраты евклидовых расстояний от этой точки до всех точек ?^l и, тем самым, отнести ее к одному из k классов. Ответом является номер нейрона, выдавшего минимальный сигнал.

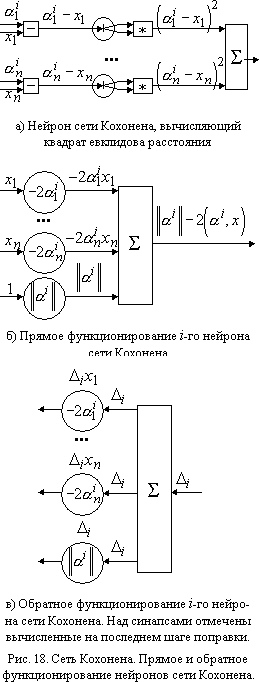
Теперь рассмотрим сетевую реализацию. Во первых, вычисление квадрата евклидова расстояния достаточно сложно реализовать в виде сети (рис. 18а). Однако заметим, что нет необходимости вычислять квадрат расстояния полностью. Действительно,

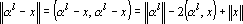
Отметим, что в последней формуле первое слагаемое не зависит от точки x, второе вычисляется адаптивным сумматором, а третье одинаково для всех сравниваемых величин. Таким образом, легко получить нейронную сеть, которая вычислит для каждого класса только первые два слагаемых (рис. 18б).

Второе соображение, позволяющее упростить обучение сети, состоит в отказе от разделения второго и третьего шагов алгоритма.

Алгоритм классификации.

1. На вход нейронной сети, состоящей из одного слоя нейронов, приведенных на рис. 18б, подается вектор x.

2. Номер нейрона, выдавшего минимальный ответ, является номером класса, к которому принадлежит вектор x.

Алгоритм обучения.

1. Полагаем поправки всех синапсов равными нулю.

2. Для каждой точки множества {xp} выполняем следующую процедуру.

 1. Предъявляем точку сети для классификации.

 2. Пусть при классификации получен ответ — класс l. Тогда для обратного функционирования сети подается вектор ?, координаты которого определяются по следующему правилу:

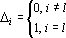
 3. Вычисленные для данной точки поправки добавляются к ранее вычисленным.

3. Для каждого нейрона производим следующую процедуру.

 1. Если поправка, вычисленная последним синапсом равна 0, то нейрон удаляется из сети.

 2. Полагаем параметр обучения равным величине, обратной к поправке, вычисленной последним синапсом.

 3. Вычисляем сумму квадратов накопленных в первых n синапсах поправок и, разделив на –2, заносим в поправку последнего синапса.

 4. Проводим шаг обучения с параметрами h₁=0, h₂=-2.

4. Если вновь вычисленные синаптические веса отличаются от полученных на предыдущем шаге, то переходим к первому шагу алгоритма.

В пояснении нуждается только второй и третий шаги алгоритма. Из рис. 18в видно, что вычисленные на шаге 2.2 алгоритма поправки будут равны нулю для всех нейронов, кроме нейрона, выдавшего минимальный сигнал. У нейрона, выдавшего минимальный сигнал, первые n поправок будут равны координатам распознававшейся точки x, а поправка последнего синапса равна единице. После завершения второго шага алгоритма поправка последнего синапса i-го нейрона будет равна числу точек, отнесенных к i-му классу, а поправки остальных синапсов этого нейрона равны сумме соответствующих координат всех точек i — о класса. Для получения правильных весов остается только разделить все поправки первых n синапсов на поправку последнего синапса, положить последний синапс равным сумме квадратов полученных величин, а остальные синапсы — полученным для них поправкам, умноженным на –2. Именно это и происходит при выполнении третьего шага алгоритма.

Оглавление книги