Книга: Учебное пособие по курсу «Нейроинформатика»
Сети Хопфилда
Сети Хопфилда
Классическая сеть Хопфилда [312], функционирующая в дискретном времени, строится следующим образом. Пусть {ei} — набор эталонных образов (i=1, …, m). Каждый образ, включая и эталоны, имеет вид n-мерного вектора с координатами, равными нулю или единице. При предъявлении на вход сети образа x сеть вычисляет образ, наиболее похожий на x. В качестве меры близости образов выберем скалярное произведение соответствующих векторов. Вычисления проводятся по следующей формуле:
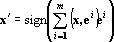
Эта процедура выполняется до тех пор, пока после очередной итерации не окажется, что x=x'. Вектор x, полученный в ходе последней итерации, считается ответом. Для нейросетевой реализации формула работы сети переписывается в следующем виде:
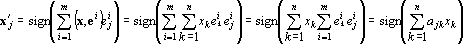
или
x'=sign(Ax),
где
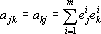
На рис. 17 приведена схема сети Хопфилда [312] для распознавания четырехмерных образов. Обычно сети Хопфилда [312] относят к сетям с формируемой синаптической картой. Однако, используя разработанный в первой части главы набор элементов, можно построить обучаемую сеть. Для построения такой сети используем «прозрачные» пороговые элементы. Ниже приведен алгоритм обучения сети Хопфилда [312].
1. Положим все синаптические веса равными нулю.
2. Предъявим сети первый эталон e? и проведем один такт функционирования вперед, то есть цикл будет работать не до равновесия, а один раз (см. рис. 17б).
3. Подадим на выход каждого нейрона соответствующую координату вектора e? (см. рис. 17в). Поправка, вычисленная на j-ом синапсе i-го нейрона, равна произведению сигнала прямого функционирования на сигнал обратного функционирования. Поскольку при обратном функционировании пороговый элемент прозрачен, а сумматор переходит в точку ветвления, то поправка равна ei?ej?.
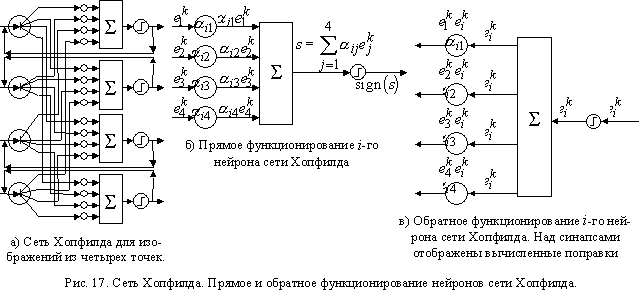
4. Далее проведем шаг обучения с параметрами обучения, равными единице. В результате получим ?ij=ei?ej?.
Повторяя этот алгоритм, начиная со второго шага, для всех эталонов получим
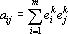
- Функционирование сети
- Сети для инвариантной обработки изображений
- Правила остановки работы сети
- Лекции 4, 5 и 6. Нейронные сети ассоциативной памяти, функционирующие в дискретном времени
- Раздел VII Левиафан в Сети: защита права на тайну частной жизни после событий 2013 г.
- Работа с ресурсами локальной сети
- 10.4. Локальные сети
- Вот как мы можем повлиять на коммерческий фактор (иными словами, повысить доверие посетителей к сайту)
- Часть II Компьютерные сети и подключение к Интернету
- Как подключить ноутбук к сети Интернет
- Часть IV Работа в сети Интернет
- Неисправности электрической сети и сетевых устройств




