Книга: Статистика и котики

Глава 4. Как понять, что песики отличаются от котиков или p-уровень значимости

Глава 4.

Как понять, что песики отличаются от котиков

или p-уровень значимости

Предположим, что вы вычислили t-критерий Стьюдента. Или U-критерий Манна-Уитни. Или какой-нибудь другой. Как же по нему понять, действительно ли песики и котики различаются по размеру? Чтобы это выяснить, статистики используют весьма нетривиальный подход.

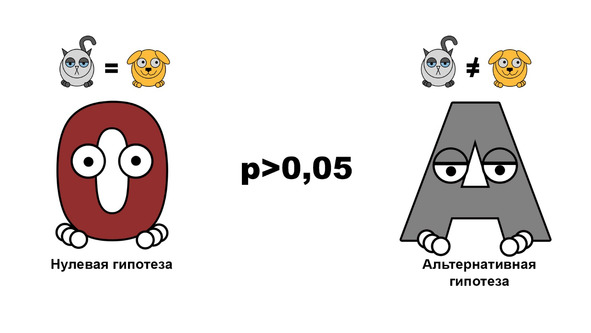
Во-первых, они делают предположение, что котики и песики, как биологические, виды абсолютно не отличаются друг от друга. Это предположение называется нулевой гипотезой.

Следующим шагом они вычисляют вероятность того, что две случайно выбранные группы котиков и песиков дадут значение критерия большее или равное тому, которое мы получили (чаще всего без учета его знака). Эта вероятность называется p-уровнем значимости.

Если p-уровень значимости меньше 5% (чаще записывается как 0,05), то нулевая гипотеза отвергается и принимается гипотеза о том, что котики и песики все-таки различаются. Такая гипотеза называется альтернативной.

Если же p-уровень значимости больше 0,05, то нулевая гипотеза не отвергается.

Однако то, что она не отвергается, еще не значит, что она верна. Это означает только то, что в данном опыте мы не обнаружили значимых различий.

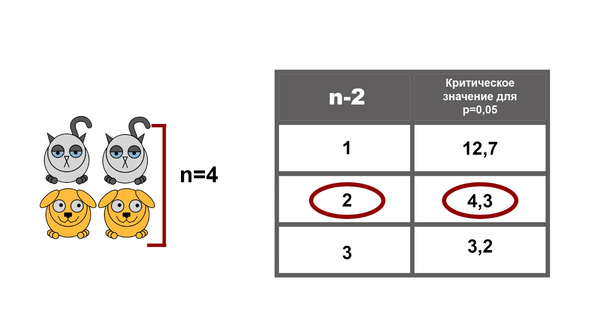
В специальных статистических программах p-уровень значимости вычисляется автоматически, и нам достаточно просто найти его в соответствующей таблице. Однако, если у вас таких программ нет, то вам придется пользоваться таблицами критических значений.

Работать с ними просто: найдите нужную строчку и посмотрите на значение критерия, которое там указано. Если то, что вы получили, превышает это значение, то котики и песики отличаются друг от друга. Правда, для этого правила есть исключения — это U Манна-Уитни и родственные ему критерии.

НЕМАЛОВАЖНО ЗНАТЬ!

Альтернативные подходы

Определение различий по p-уровню значимости в последнее время подвергается жесткой критике. Поэтому немаловажно знать о том, что существуют и альтернативные подходы, которые используются при определении значимости полученных результатов.

Доверительные интервалы. Как уже было сказано ранее, ученые чаще всего проводят свои исследования не на всех котиках, а на какой-то выборке. Соответственно, они не знают истинного среднего размера по всем котикам. Однако они могут прикинуть, в каком диапазоне он находится. Такой диапазон называется доверительным интервалом.

Рядом с доверительным интервалом всегда указывается вероятность. 95%-ый доверительный интервал означает, что мы с точностью в 95% можем утверждать, что истинный средний размер котиков находится в этом диапазоне.

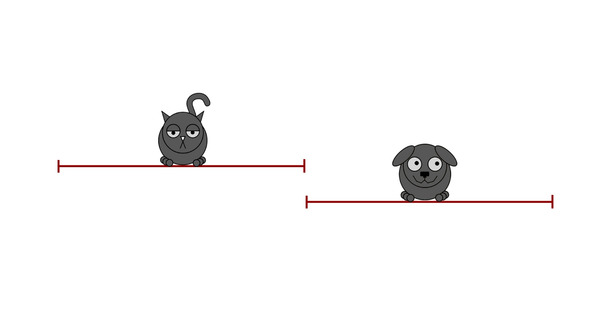
Чем шире такой интервал, тем менее точной считается статистическая оценка. Что касается различий между песиками и котиками, то они имеют место быть, когда их доверительные интервалы не пересекаются.

Байесовская статистика. Все вышеприведенные способы определения значимости не учитывают наши предыдущие (априорные) знания о том, каких размеров бывают котики и песики. Каждый раз, когда мы определяем p-уровень значимости или доверительный интервал, мы ведем себя так, как будто никогда не видели ни тех, ни других.

Но ведь это не так! Мы ведь достаточно четко представляем себе, как они выглядят! Нельзя просто так брать и отбрасывать предыдущий опыт!

Проблему сопоставления наших предыдущих знаний и новых данных пытается решить группа методов, основанных на теореме английского священника Томаса Байеса.

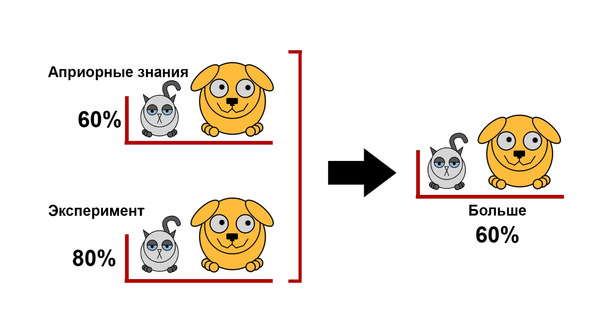
Не вдаваясь в математические подробности, опишем общую логику. Предположим, что из предыдущих опытов мы выяснили, что в 60% случаев случайно выбранный песик больше случайно выбранного котика. Проведя собственный эксперимент, мы обнаружили, что это число гораздо выше — 80%. Следует ли из этого, что нам нужно забыть наш предыдущий опыт и заменить старые данные новыми? Разумеется нет. Новый опыт только подправит предыдущую вероятность, и в следующий раз мы будем считать, что она несколько выше.

Оглавление книги